الوسم: الغير

نشاط1:
1
الشرح:امتناع اتباع الشيطان لوجود فضل الله ورحمته
2
الشرح:امتناع القضاء بينهم لوجود كلمة الحق
3
امتناع مجيء العذاب لوجود الاجل
4
امتنع البديل لوجود طلاب العلا
5
امتناع رؤية اللقاح لوجود الرياح
6
امتناع الظلام الدامس على الانسانية لوجود العلم

نشاط2:
– لماتت الكائنات
– لما صاحبتك
– لما نشأوا صالحين

ويرمز لهذه العملية حسب اصطلاح لورينتز :

.

النقطة الأساسية في التكامل تأتي من المبرهنة الأساسية في التكامل والتي تنص على أن مشتق تابع المساحة تحت منحني الدالة هو الدالة نفسها. بالتالي إذا عرفنا دالة تربط القيمة x يقيمة المساحة المحدودة بين منحني الدالة ومحور السينات ومن الجهة الخرى محدودة بمحور العينات والمستقيم X=x، تدعى هذه الدالة ب دالة المساحة ومشتقها هو الدالة نفسها، لذلك ندعو تابع المساحة عكس الاشتقاق أو التابع الأصلي للدالة .

يقوم حساب التكامل على إيجاد التابع الأصلي للدالة التي نريد القيام بمكاملتها.

وقد عرض جوتفريد لايبنتز، في 13 نوفمبر 1675، أول عملية تكامل لحساب المساحة تحت منحنى الدالة ص = د(س).

يوجد عدة أنواع للتكامل منها: التكامل بالتجزئ ،التكامل بالتعويض، التحويل إلى الكسور الجزئية، الاختزال المتتالى

[عدل] التكامل ماقبل عصر علم التفاضل والتكامل

توجد دلالات تاريخية على استخدام التكامل في عهد قدماء المصريين (حوالي 1800 قبل الميلاد) فقد دلت بردية موسكو الرياضية على علمهم بصيغة لحساب حجم الهرم المقطوع. وتعد طريقة الاستنزاف من أوائل الطرق المستعملة في إيجاد التكاملات حيث تعود إلى 370 قبل الميلاد وكانت تحسب بها الحجوم والمساحات وذلك بتقسيمها إلى أشكال صغيرة غير منتهية معلومة المساحة أو الحجم. كما تم تطوير هذه الطريقة أكثرمن قبل أرشيميدس واستعمالها في حساب مساحات القطع المكافئ وتقريب لمساحة الدائرة. وفي الصين طورت طرق مماثلة في القرن الثالث الميلادي بواسطة ليوهوي, والذي استخدمها لإيجاد مساحة الدائرة كما تم استعمال هذه الطريق فيما بعد في القرن الخامس من قبل الرياضيين الصينيين – الأب والابن تسوتشونغ وزوجنغ لإيجاد حجم الكرة.[1] في نفس القرن, استخدم الرياضي الهندي اريابهاتا طريقة مشابهة لحساب حجم المكعب.[2]
أتت الخطوة التالية والهامة في التفاضل التكاملي في القرن الحادي عشر عندما أخترع الحسن بن الهيثم مابات يعرف اليوم مسألة الحسن (نسبة لاسمه المشهور عند الأوروبيين) والتي تقود إلى معادلة الدرجة الرابعة. في كتابه المناظر. بينما كان يحل هذه المسألة, قام بعملية تكامل لإيجاد حجم السطح المكافئ. وقد استكاع بالاستقراء الرياضي تعميم هذه النتيجة لدوال كثيرة الحدود حتى الدرجة الرابعة وقد كان بالتالي قادرا على إيجاد صيغة عامة لتكاملات كثيرة الحدود ولكنه لم يعر أهمية لذلك انذاك.[3] بعض الفكر في التفاضل التكاملي يمكن مصادفتها أيضا في سيدهانتا شيروماني, وهي عبارة عن نص يعود للقرن الثاني عشر للفلكي الهندي بهاسكارا 2.
لم يبدأ ظهور التقدم الملحوظ في علم التكامل التفاضلي إلا مع القرن السادس عشر وفي هذا الوقت كان عمل كافاليري بطريقته الكل لا التجزيء وعمل فيرمات, بدأ بوضع الأساسات لعلم التفاضل والتكامل الحديث. كان لإسحق نيوتن وتورشيلي دورا هاما أيضا في توسيع هذا العلم أوائل القرن السابع عشر اللذان قدما التلميحات الأولى في وجود صلة بين التكامل والاشتقاق في الوقت الذي كان الرياضيون اليابانيون قد أسهمو في أعمال مثيله وبشكل خاص على يد سيكي كاوا.[4] كان منها طرق إيجاد مساحات الأشكال بالتكامل, بتوسيع طريقة الاستنزاف.
[عدل] نيوتن وليبنز

مثل اكتشاف النظرية الأساسية للتفاضل والتكامل الفريد من قبل إسحاق نيوتن وليبنيز تقدما عظيما في علم التفاضل والتكامل. فهي توضح العلاقة بين التكامل والتفاضل. هذه العلاقة, بدمجها مع قرينتها السهلة – الاشتقاق يمكن استغلالها لحساب التكاملات. وبشكل خاص فإن النظرية الأساسية للتفاضل والتكامل تساعد في حل مسائل أكثر تعقيدا. وبإعطاء اسم التفاضل المتناهي في الصغر فقد سمحت بتحليل دقيق لدوال متصلة. لقد أصبح هذا العمل التفاض والتكامل الحديث, والذي استمد رمزه من عمل ليبنيز.
[عدل] صياغة التكاملات

مع أن نيوتن وليبنز أوجدا طريقة نظامية للتكامل إلا أن عملهما كان يفتقر إلى درجة الدقة. فقد هاجم جورج بركلي عبارة متناهي في الصغر ووصفها بكميات الأشباح المغادرة. اكتسب التفاضل والتكامل مع تطور علم النهايات وتوطدت أركانه بفضل أوغستين لويس كوشي في منتصف القرن التاسع عشر. تم أولا صياغة التكامل بدقة باستعمال النهايات من قبل بيرنارد ريمان كما ظهرت صورة أخرى من قبل هنري ليبزغ في تأسيس نظرية القياس.
[عدل] العلامة

استعمل نيوتن عمودا صغيرا فوق المتغير للإشارة إلى عملية التكامل, أو أن يضع المتغير داخل مربع. كان القضيب العمودي يلتبس مع و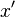, والتي كان قد استعملها نيوتن للإشارة للتفاضلكما كان من الصع على الطابعة التعامل مع المربع, وبالتالي لم يتم تبني هذه العلامات. الرمز الحديث للتكامل الغير محدود تم تقديمه على يد ليبنيز عام 1675 (Burton 1988, p. 359; Leibniz 1899, p. 154), كما أنه قام بموائمة رمز التكامل,:, بعد إطالته للحرف s كتمثيل لاختصار عملية الجمع sum. الشكل الحديث لعلامة التكامل المحدود استعمل لأول مرة من قبل جوزيف فوريير بإضافة حدود التكامل أسفل وأعلى الرمز السابق (Cajori 1929, pp. 249–250; Fourier 1822, §231).
الجدير بالذكر أن الرياضيات العربية التي تكتب من اليمين لليسار تستعمل الرمز المعكوس للتكامل, ، ليتماشى مع اتجاه الكتابة.(W3C 2022).
[عدل] مقدمة

تظهر التكاملات في العديد من الحالات التطبيقية. إذا اعتبرنا بركة السباحة مثلا, إذا كانت مستطيلة الشكل, من طولها, عرضها, وعمقها فمن الممكن إيجاد حجم الماء التي يمكن احتواؤها (لملئها), مساحتها السطحية (التي تغطيها من جميع الجهات), وطول حوافها (بحبل مثلا). لكن إذا كانت بيضاوية الشكل ومدورة من القعر, فإن كل هذه الكميات تستدعي التكامل. قد تكون التقريبات التطبيقية كافية في مثل هذه الأمثلة البسيطة ولكن الدقة الهندسية تتطلب قيما مضبوطة ودقيقة لهذه العناصر.

تقريب التكامل لـ √x من 0 إلى 1, بـ■ 5 عينات على اليمين (فوق) و■ 12 عينة على اليسار (أسفل)

للبدء, اعتبر المنحنى بين x = 0 وx = 1, و. يكون السؤال:
ماهي المساحة تحت الدالة f, في الفترة 0 إلى 1? ولندعي أن هذه المساحة (حتى الآن غير معلومة) هي تكامل f. يكون الرمز لهذا التكامل هو:
كتقريب أولي فلننظر في مربع الوحدة المعطى بالأضلاع x = 0 إلى x = 1 و nbsp;= 0 and y = f(1) = 1. مساحته هي 1 تماما. ينبغي أن تكون القيمة الحقيقية للتكامل أقل مما هي عليه. بتقليل عرض المستطيلات التقريبية يعطي نتيجة أفضل, وبالتالي عبر الفترة في خمس خطوات, باستعمال نقاط التقريب 0, 1⁄5, 2⁄5, وهكذا حتى 1. بوضع مربعا مناسبا لكل خطوة مستخدمين الارتفاع المناسب لكل قطعة منحنية، وعليه 1⁄5√, 2⁄5√, وهكذا حتى 1√= 1. وبجمع مساحات هذه المستطيلات, نحصل على تقريبا أفضل للتكاملات المقصودة,
لاحظ أننا نأخذ مجموع لقيم دوال عديدة محدودة لـ f, مضروبة في الفرق بين فترتين تقريبيتين متعاقبتين. يمكننا ملاحظة أن التقريب ما زال كبيرا. وكلما استخدمنا خطوات أكثر حصلنا على تقريبات أفضل, ولكننا لن نحصل على قيم دقيقة أبدا: بإبدال الـ5 فترات بـ12 فترة نحصل على التقريب 0.6203, وهي تقريب أفضل. مفتاح الفكرة يكمن في الانتقال من العديد من نقاط التقريب المحدودة مضروبة بقيم دالتها إلى استعمال عدد لانهائي أو خطى متناهية في الصغر. بالنسبة للحساب الحقيقي للتكامل, تكون النظرية الأساسية للتكامل هي الرابط الأساسي بين عمليات الاشتقاق والتكامل. وبتطبيقها على منحنى الجذر التربيعي,f(x) = x1/2, تقترح علينا أن نبحث عن المشتق العكسي F(x) = 2⁄3x3/2, ونأخذ ببساطة F(1) − F(0), حيث 0 و1 هي حدود الفترة [0,1].هذه حالة لقاعدة عامة, لإجل f(x) = xq, مع q ≠ −1, تكون الدالة المتعلقة والتي تدعى المشتق العكسي هي وبالتالي فإن القيمة الدقيقة للمساحة تحت المنحنى رسميا كما يلي
[عدل] تعريفات منهجية

هناك عدة طرق لتعريف التكامل بشكل منهجي, لكن هذه الطرق مختلفة عن بعضها البعض في الطرق التي تسلكها. بعض هذه الإختلافات ننجت عن محاولات الرياضياتيين لحل حالات خاصة من المسائل التي تكون فيها المسألة غير قابلة للتكامل, و بعضها الآخر نتجت لأسباب تعليمية -كتسهيل حل المسائل-. إن أكثر تعريفين شيوعاً للتكامل هي تكامل ريمان وتكامل لوبيغ.
[عدل] تكامل ريمان

مقال تفصيلي :تكامل ريمان

صورة توضيحية لتكامل تقريبي عند إستخدام مجموع ريمان, تم تقسم المساحة الموجودة تحت المنحنى إلى مضلعات غير منتظمة (الضلع الذي يوجد تحته الخط الأحمر هو الأعرض). القيمة الدقيقة للمساحة هي 3.76; و القيمة الفرضية هي 3.648.

يمكن تعريف تكامل ريمان على أنها أخذ مجموع ريمان للدالة الموجودة ضمن مجال جزئها المحدد Tagged partition. فإذا كان الفترة [a,b] هي فترة مغلقة في خطها الحقيقي; فإن جزئها المحدد ضمن الفترة [a,b] هي سلسلة متناهية، حيث تكون:

صورة توضيحية لمجموع ريمان عندما يتم تقسيم فترات مساحة الأضلاع إلى نصفين في كل مرة، لاحظ بأن القيمة التقريبية تزداد صحةُ كلما أزداد عدد الأضلاع.

وهذا سيجزأ الفترة [a,b] إلى n جزء ذو الفترة الجديدة [xi−1, xi]، حيث أن i يعتمد على عدد الأجزاء, كل واحد من هذه الأجزاء "تم تحديدها" بنقطة مفرِّقة ti التي تنتمي للفترة [xi−1, xi]. إذاً، تُعرّف مجموع ريمان للدالة f الموجودة ضمن الجزء المحدد من الفترة [a,b] على النحو التالي:
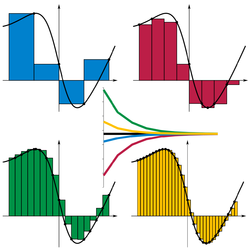
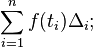و بالتالي، كل حد من المجموع هي عبارة عن مساحة لمضلع لديه إرتفاع تساوي قيمة الدالة عند النقطة المفرقة للجزء المعطى, و لديه عرض تساوي طول الفترة الجزئية. فلتكنΔi = xi−xi−1 هي عرض الفترة الجزئية i; لكي يكون تشبيك هذا النوع من الأجزاء المحددة هي نفسها عرض أكبر فترة جزئية تم تشكيلها بواسطة التجزئية, التي لها القيمة القصوى i=1…n Δi. إذاً، تكامل ريمان للدالة f في الفترة [a,b] هي مساوية للقيمة S: فإذا كان جميع قيم ε > 0، ستكون جميع قيم δ > 0. وإذا كان هناك جزء محدد في الفترة [a,b] أقل من قيمة δ, ستكون:
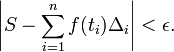المصادر[LIST=1]<LI id=cite_note-0>^ Shea, Marilyn(مايو 2022),Biography of Zu Chongzhi, University of Maine, <http://hua.umf.maine.edu/China/astronomy/tianpage/0014ZuChongzhi9296bw.html>. وُصل إليه في 1 يناير 2009
Katz, Victor J.(2004),A History of Mathematics, Brief Version, Addison-Wesley, pp. 125–126, ISBN 978-0-321-16193-2 <LI id=cite_note-1>^ Victor J. Katz (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163-174 [165] <LI id=cite_note-Katz-2>^ Victor J. Katz (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163–174 [165–9 & 173–4] [*]^ http://www2.gol.com/users/coynerhm/0598rothman.html[/LIST]

http://ar.wikipedia.org/wiki/%D8%AA%…A7%D9%85%D9%84

ارجو تعديله

أ جيبي :

ماذا يحصل لحركة جسم حين تؤثر فيه قوى غير متزنة ؟
………………………………………….. ………………………………………….. …

ماذا يكون قد حصل لجسم حين تراه يغير حركته ؟
………………………………………….. ………………………………………….. ……………….

ما حصله القوى حين تدفع قوة تساوي 100نيوتن مقابل قوة احتكاك تساوي 80 نيوتن

………………………………………….. ………………………………………….. ……………….

ما هي محصله القوى ؟

………………………………………….. ………………………………………….. ……………………….

معهد الإمارات التعليمي

ويكبيديا الموسوعه الحره